Location
Manhattan, NY
Typology
Manhattan Block
Size
80m x 180m
Function
Mixed-use
Constructing the Manhattan Gene
The Manhattan Block
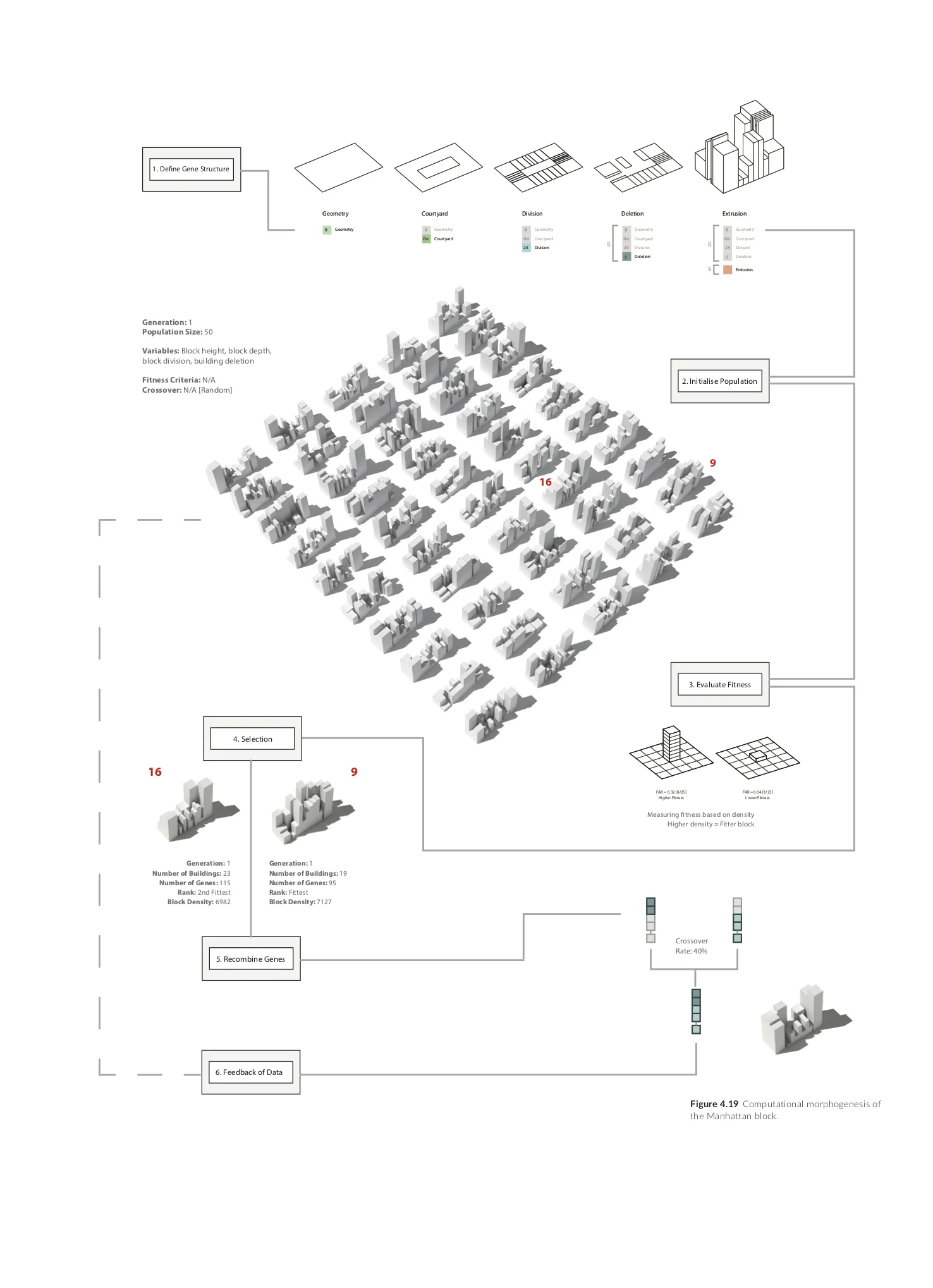
The average Manhattan Block is 80 meters x 180 meters. The block has been designed with a gene pool of 5 variables that control the geometrical footprint of the block, the division of the block into buildings, the block’s depth, height and the number of buildings that are deleted from the block (figure at the top). The research focuses on the relationship between the sequencing of genes and their output as differentiated blocks. The phenotype is analysed and ranked while all changes on the design level take place at the gene level. A random population of 40 individuals were initially created whose genes were randomly sequenced. In each generation, the phenotype is analysed and ranked according to the fitness criteria. The fitness criteria in this case is density – the higher the density of the block, the fitter it is. The diagrams on this board only show the first generation and the recombination of two individuals from that population. The graph below illustrates the fitness of each population over 7 generations. It can be seen that the individuals gradually converge as a population.
Evolutionary computation of the Manhattan block
Fitness Criteria
The structure and sequence of this data leads to differentiated physical outcomes (or phenotypes). Therefore, algorithms are used to construct what can be referred to as digital genomes (figure 1) in simulating complex behaviours (i.e. patterns of self-organisation) and constructing complex systems. It illustrates how digital genomes can be used to generate differentiated phenotypes and populations of digital objects (blocks) in design. The data structure defines and manipulates spatial and geometrical characteristics of a design model.
The Manhattan Superblock
Superblock
In this section, the experiments at the scale of a superblock. There is no speci c number for how many blocks compose a superblock, although superblocks tend to be at a scale of about 16 acres [800m x 800m] (Shane, 2014). The genes of a superblock will have to be recon gured and small computa onal adjustments will have to be made from that of a single block. Superblocks will vary in gene structure. One example is the addi on of path systems that divide and connect blocks to one another (Figure 4.29 on page 130) . A single block does not require such a gene as there is no need to connect it to other blocks. The use of superblocks in design may be more bene cial for environmental calcula ons and massing studies, allowing for the environmental consequences of mul ple blocks to be taken into considera on all at once.
Figure 4.30 on page 131 illustrates the composi onal structure of the Manha an superblock as a 3x4 grid [440m x 810m]. As a result, the number of genes is at least 12 mes higher than a single block, requiring more computa on me to calculate di erent varia ons of each block as well as di erent sequences in gene recombina on. In this sequence of experiments, the focus will also shi from a single-objec ve criterion to mul -objec ve criteria. In the previous sequence, the objec ve was density whereas in this sequence the objec ves include density (popula on per hectare), shadow analysis (the amount of light that is able to penetrate to the street level) and spaciousness (how spacious the ssue feels at ground level) (Figure 4.13 on page 112). The objec ves are contradictory in certain cases, for example, density and spaciousness are aimed at opposite objec ves, so rather than convergence towards an op mal solu on, the gene c solver will generate a popula on of solu ons that perform well in di erent areas. It is up to the designer to select what best ts the design scenario.
Multi-objective criteria optimisation
Generation IGeneration 30The Manhattan
Tissue
This phase of the experiment focuses on a much larger scale of the city from a 810m x 440m superblock to a 7km x 4km ssue. The number of blocks will increase from 12 blocks to 690. The poten al number of buildings will increase from 252 to 14,490. Each building has a genome composed of 5 individual genes, a total of 72,450 genes not including the genes for regula ng street widths. The change in scale will cause a signi cant increase in the computa on power required for the genera on of such a ssue. There are two approaches that can be taken with the genes: the rst is to create every gene individually and de ne their upper and lower bounds, being that they are primi ve data such as integers or doubles. The second is to rely on a random number generator. The random number generator would make for an easier solu on in construc ng the data structure of the ssue but the evolu onary solver would have no way of actually evolving genes as it would only change the seed value of the random number generator. The seed value is simply used as a mechanism to generate random numbers. Evolu onary models rely on the changing of gene values to gauge tness measures within a search space. In other words, if an evolu onary solver was evolving a block with a single height gene, it would know that increasing the height gene will allow the solu on to have a greater tness value in the search space. However, if the height gene was controlled through a random number generator, the evolu onary model would increase the seed value and the random number generator would generate a purely random value, poten ally lower or higher height than the number before. The random number generator has no correla on with the search space and as a result its applicability would have no value in this case. Thus, the data structure will rely on the crea on of individual genes for this design exercise.